Openfabric economy

In most economic systems, the products and services carry a built-in layer of knowledge that is indistinctive from the rest of the system, blurring the real value of the intelligence. Openfabric creates a novel form of economy which exploits the intelligence in its purest form. In Openfabric’s economy, knowledge represents the primary governing factor and fundamental value system. The critical element in propelling the law of accelerated returns [48] is to design appropriate incentive mechanisms [49] that empower innovators to monetize their work and encourage collaborative exploration and research. Building a genuinely sustainable economy of intelligence [50] requires securing a high degree of quality and performance for all network services.

A. Economic Interactions

Openfabric provides a built-in peer-to-peer marketplace that facilitates transactions between main stakeholders, as depicted in Table I:

• The service consumer uses the network to get solutions toward particular business problems carrying the expense for AI and execution services.
• The infrastructure provider rents the execution environment to run AIs, and is getting paid on a per-execution basis, in accordance to the amount of hardware resources being utilized.
• The AI Innovator adds value to the network by developing and deploying AI solutions capable of solving demanding problems, being paid each time that the implemented AI is executed.
• The data providers own the relevant data that can be used during the process of AI training; they are getting paid each time their datasets are downloaded.

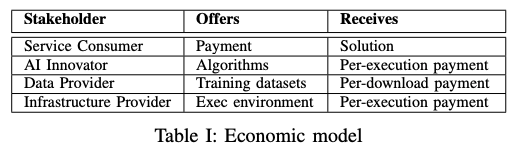
Table 1 - Economic model

The economic exchange between parties utilizes a pay-perexecution model based on an intrinsic token. Each actor that performs commercial operations on the platform possesses an account (a simple public/private keypair, used to sign transactions) and - optionally - a wallet (smart-contracts that allow advanced features, such as transaction logging, multisig, withdrawal limits, and more) [51].

B. Payment System

The payment system must guarantee the fair, fast and secure transfer of funds between parties, when doing transactions. The protection of all involved parties needs to be enforced at the protocol level. The receiver needs the guarantee that the sender has the available funds to pay, and that they will get paid once the job has succeeded. The sender requires that they pay only if the job is concluded successfully, in a specified time frame. Fostering an improved user experience can be accomplished by diminishing the response and bootstrap (execution startup) times. For the end-user, the system response should be almost instantaneous, which is achievable by the combination of an escrow smart-contract [21], [52] and unidirectional atomic payment channels. A payment channel [53], [54] enables the secure off-chain transactions between parties without blockchain delay. Considering the simple flow displayed in Fig. 4:

1. Alice (service consumer) deposits funds into the escrow smart-contract with a specific withdrawal timeout. She can recover the funds only after the timeout has passed;
2. Alice opens a payment channel with the system (DOS);
3. Alice submits a signed request to run an AI algorithm employing a time-bound execution environment configuration EE;
4. The system checks whether Alice has the required funds in the escrow;
5. The system will send a message to Bob (infrastructure provider) to prepare the execution;
6. The system will lock the funds required for the execution for a time frame;
7. Alice sends the input data over a TLS connection, Bob starts the execution of AI;
8. If Bob has successfully concluded the task, the payment channel will be closed, and funds will be released into his account;
9. If Bob was unable to perform the job in the allocated time frame, the funds would be unlocked.

The above-presented design poses some limitations in enforcing the closing of the channel before the funds can be released. This approach affects the overall performance, and may introduce some significant delays [55], especially in the case of batch execution. The path to solving this limitation is to add a nonce to the channel, which will act as a wrapper containing the general commitment and expiration timeout. Inside the main channel, subchannels will be spawned, with each one possessing its commitment and timeout. The channel nonce and expiration timeout will be updated each time a new request is initiated. Alice can submit multiple execution requests, with each one being processed separately. Following this approach, the payment channel possesses the following favorable characteristics:

• The channel between parties can persist considerably;
• The sender can add funds to the channel and extend the expiration timeout, as needed;
• The recipient can claim the agreed-upon amount at any time;
• The underlying blockchain system delays will not affect the transactions between parties.

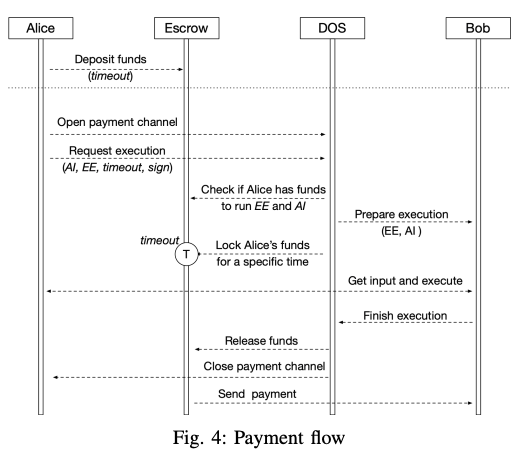
Fig. 4: Payment flow

C. Incentive Mechanism

Achieving the Nash equilibrium [36], [56] in a decentralized ecosystem that fosters collaborative innovation implies the use of a built-in, self-regulatory reward system. Fueling the chain reaction which propels the ecosystem toward fast and sustainable growth, the incentive mechanism behind it must solve the well-known network-effect bootstrapping problem [57]. Openfabric empowers innovators on creating novel solutions by piecing together functionalities of the previously-deployed algorithms. Fig. 5 depicts the dependency structure in which the root algorithm $u$ makes use of the children sub-algorithms $q_i$. In turn, each child algorithm may integrate further subalgorithms.

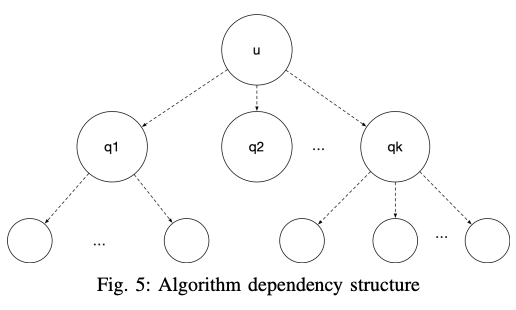
Fig. 5: Algorithm dependency structure

Openfabric utilizes an incentive tree mechanism [58], [59] that encourages cooperation over competition. All algorithms in the tree at any level will be rewarded, while keeping a fixed cost for the end-user. $T_u$ represents the sub-tree rooted at node $u$ having $k$ children $q_1$,...,$q_k$, $T_ {uq}$ represents $T_u$'s first level children. The total cost of the $T_u$ can be computed as:

$Cost(T_u)= p_{u} + \sum_{i=1}^{k}{C(q_i) * p_{q_i}}$

where pu represents the node cost (specified by the innovator), and C(qk),(0 ≤ C(qk) ≤ 1) represents the contribution function of the node qk. Computing the C(qk) function requires considering the general rating of the algorithm, the relative position in the current tree, and how often other algorithms use the algorithm qk. Given the total contribution C(T) and π(x) functions defined below:

$C(T)= \sum_{u \in T_q}{C(u)}$

$\pi(x)=\beta x + (1-\beta)x^{1+\rho}$

the reward function R(u) [60] is defined as:

$R(u)= \Phi C(T) \left [ \pi(\frac{C(T_u)}{C(T)}) - \sum_{T_{qi} \in T_{uq}}{\pi(\frac{C(T_{qi})}{C(T)})} \right]$

where $\Phi (0 \leq \Phi \leq 1)$, $\beta (0 \leq \beta \leq 1)$ and $\rho (\rho > 0)$ are system parameters controlling participant reward distribution.

The designed reward mechanism possesses the following properties:

• Truthfulness: no one could increase it's utility by acting maliciously;
• Sybil-Proofness: no one could benefit from generating multiple fake identities;
• Individual Rationality: no algorithm has a negative utility in being used as a sub-algorithm.