Security

Openfabric utilizes cryptographic methods aiming to establish a secure environment that is hardened against malicious attacks or any arbitrary misuse of the system by either external or internal entities. Cryptography assumes that any protocol execution is subject to permanent aggression from malicious actors that are striving to obtain information about the system and users, tamper with data, or get unprivileged access to any resource. From a security perspective, the fundamental requirements which must be addressed by any system are privacy and correctness. Private data must be kept undisclosed to any unauthorized actor. The successful execution of a protocol should produce correct, consistent, and predictable outputs for all participants. The main security features that any decentralized system should possess are:

• Privacy - there should be no party learning, accessing, or modifying information that is not intended for that particular party;
• Correctness - it must be guaranteed that each party receives the correct output from the execution of the algorithms;
• Independence of Inputs - the inputs of the used algorithms must be independent between the honest and the corrupt parties;
• Guaranteed Output Delivery - this property states the resistance of the system to a denial of service attacks;
• Fairness - all of the parties should receive the output of the algorithms, regardless of their behavior (fair or malicious).

A. Permission Levels

Openfabric transparently regulates interactions between multiple stakeholders, but also ensures privacy and protects personal information, intellectual property, and other sensitive data. In order to preserve confidentiality and security, Openfabric implements an access control mechanism over the DLT based on smart contracts. It uses similar approaches to the one from [98] (implements a GDPR-compliant personal data management scheme in a decentralized environment) and in [99] (enhances privacy at the blockchain level), where the Access Control List (ACL) is implemented by a smart contract. Access control flow in Openfabric:

• Resource submission (e.g. AI algorithm from an AI innovator). The platform checks the requester certificate, generates encryption keys, and stores the encrypted resource off-chain. The ACL smart contract is updated to grant the requester full access to their resource.
• ACL update. Resource permissions can be modified only by the resource owner; when some other contracts are executed, the owner can decide to grant/revoke access to their resources.
• Resource retrieval. The requester interrogates the ACL smart contract. The smart contract will verify whether the requester has the necessary permissions to access the specified resource, and will grant access to it in that case.

B. Identity Management

Currently, various privacy and security regulations try to protect the user’s identity, reduce identity fraud, and strengthen online anonymity. The state of the art in identity management is the Self-Sovereign Identity (SSI) [100] model, which aims to ensure the user’s control and sole ownership over their digital identity. To implement SSI, the majority proposed solution is based on decentralized technology [101] [102] [103]. There is a trade-off between using the ideal self-sovereign identity model - in which users are the exclusive owners of all their data - and having users’ public attributes continually available, even when they are offline. The Openfabric ecosystem uses an identity management scheme based on the Public Key Infrastructure (PKI). Personal information is encrypted with the platform’s key (E), which is uniquely generated for each case separately. Fig. 13 describes stakeholders or assets identification and how the payload regarding their identity is stored. In Openfabric, the pointers to the off-chain data (H) are encrypted in a manner similar to the one described in [86]. The following steps should be performed for user registration:

• The user creates a pair of secret / public keys (sk, Pk) on their local device. The secret key should never leave the client’s device. The user’s public key (PK) represents his / her identification across the system.
• After the local key generation step, the user requests new certificates from the KYC / CA module. Certificates are used for granting and revoking access to the platform.
• The user demands an encryption key from the DOS. The DOS prompts the Secret Store to produce a pair of keys, and the newly-generated secret key will remain in the Secret Store, split among the Store’s nodes - whereas the public key (E) is forwarded to the user. On chain, the ACL is updated to link the user to this encryption key.
• The user encrypts information with the Secret Store encryption key (E), then makes a request to the DOS for storing this information. The DOS persists the payload off-chain, and on-chain, it stores a tuple with the following information: user’s public key (Pk), encryption public key (E), resource pointer (hash/address (H) of the resource), and - optionally - an identifier (required for asset identification).

The asset (AI algorithms, datasets) identification model uses a design similar to the stakeholder model, with the following difference: it does not need to generate a pair of keys (sk, Pk), because assets will use the author’s keys. Identifiers for the assets are unique across the system, and will be regenerated with each update.

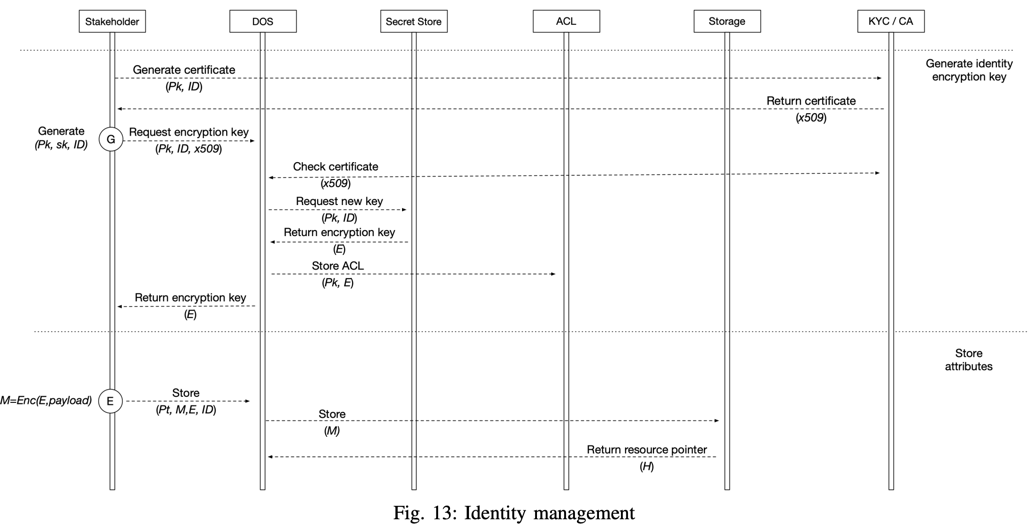
Fig.13: Identity management

C. Remote Attestation

Remote attestation [77] allows a server (Infrastructure Provider Enclave) to convince the others that the software is secure and that it is running inside an up-to-date SGX enclave. Successful attestation assures the requester of the software’s identity, and also informs about possible software tampering. For Intel SGX, there are currently two supported types of remote attestation: Intel SGX attestation service based on Intel Enhanced Privacy ID (Intel EPID), and ECDSA-based attestation based on Intel SGX DCAP. The first solution uses Intel EPID provisioning services, and requires that the platform has internet access. In contrast, the second one uses a custom implementation for SGX attestation, either because internet-based services cannot be accessed, or because the attestation process should remain in-house.

D. Key Management in Openfabric

Managing keys across a decentralized system is an endeavor that each decentralized platform should handle, if private processing of data is involved. Most centralized solutions use specialized hardware for secure storage (HSM) or custom implementations that require a trusted authority - but for the decentralized platforms, there are fewer solutions. Ethereum, Ocean Protocol [26] use the Secret Store [104] for key management, which is based on threshold cryptography and secret sharing schemes. Openfabric uses a model akin to the Secret Store for managing the platform’s keys. Fig. 14 describes the platform key generation process. The actor (any stakeholder, smart contract, or other entity) generates an ID, and requests a new key for it, specifying the key threshold. The threshold ($t$) represents the maximum number of nodes that cannot reconstruct the key. The actor signs this request with their secret key ($A_{Sk}$). Using the ECDKG [105] algorithm, a new key is generated, and each peer from the Secret Store will receive a fragment of the key. Any node belonging to the Secret Store can compute the public key ($S_{PK}$) related to the shared key.

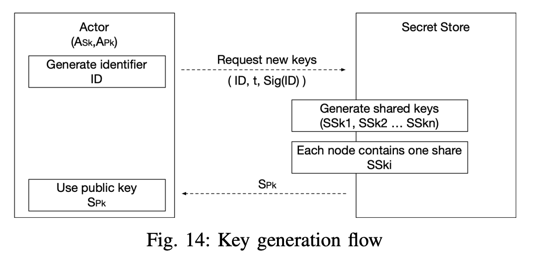
Fig.14: Key generation flow

The process of retrieving the key from the Secret Store is described in Fig. 15. Openfabric has a permission mechanism that performs Secret Store key access control. Any actor who requests a key for a specific identifier ($ID$) signs the request with their private key ($A_{Sk}$). Any of the Secret Store's nodes can check permissions for the actor's key and selected $ID$; if the approval is declined, the actor will not receive the key. Otherwise, the Secret Store network computes the key (at least $t+1$ peers from the network are required, where $t$ is the threshold of the key), and it then encrypts the key, along with the public key of the actor ($A_{Pk}$).

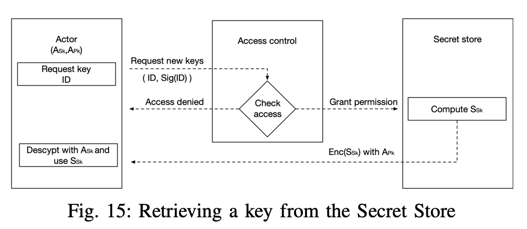
Fig.15: Retrieving a key from the Secret Store

The distributed verifiable secret sharing scheme

is a mechanism which ensures the generation, storage, and retrieval of keys in a decentralized context. ECDKG [105] represents an enhancement of the DF-VSS [106] that can tolerate halting, eavesdropping, static malicious, replay, and adaptive adversaries. Each involved party chooses its random polynomials, computes and broadcasts shares, verifies shares from the other parties, and computes its private share of the secret. None of the parties can determine the secret by itself. To successfully reconstruct a secret, the Secret Store peers must collaborate and combine $t + 1$ shares.

Elliptic curves

represent a particular subset of mathematical equations of the following form: $y^2=x^3+ax+b$, and displaying some unique characteristics with regards to cryptographic operations. In the equation above, the coefficients $a$ and $b$ control curve behavior. Operations such as addition, multiplication by scalars, etc. applied on any curve point $T(x,y)$ will keep the results inside the group $\left(G,\bigoplus\right)$.

ECDKG algorithm

• Notation: All arithmetic operations are done in a finite field $GF(q)$, $G$ is the additive group derived from point $T$, and $\bigoplus$ is the addition operator over $G$. $\sum_{}^{ \, \bigoplus}$ represents point summation.

• Key distribution:

  • Setup: For generating a second point $T'$, each of the n parties chooses a random number $r \in GF(q)$, then sets:
    $T' = \sum_{i=1}^{n \, \bigoplus}{r_iT}$
  • Polynomials generation: Each party $p_i$ generates two random polynomials $f_i$ and $f_i'$ over $GF$ of degree $t$. $f_i(z)=\sum_{k=0}^{t}a_{ik}{z^k} \;, f_i'(z)=\sum_{k=0}^{t}b_{ik}{z^k}$
  • Compute public shares: Compute $P_{ik}$ for $0\leq k \leq t$. Broadcast them to all parties. $P_{ik} = (a_{ik}T)\bigoplus(b_{ik}T')$
  • Compute private shares: Each $p_i$ secretly shares the $s_{ij}$ and $s'_{ij}$ with $p_j$, for $j=1,2, \dots, n$: $s_{ij} = f_i(p_j)\,mod\,p \;, s_{ij}' = f'_i(p_j)\,mod \, p$

• Key verification:

  • Verify: Every party $p_j$ verifies the shares received from the other parties $p_i$. $(s_{ji}T)\bigoplus(s'_{ji}T') = \sum_{k=0}^{t \, \bigoplus}{p_i^kP_{jk}}$ with $i=1,2,\dots,n$. If validation fails for a specific index $i$ the $p_j$ party broadcasts complains against $p_i$.
  • Dispute: If more than $t$ participants complain against $p_i$, then $p_i$ is considered faulty, and is excluded. Otherwise, the $p_i$ will reveal shares $s_{ij}$ and $s'_{ij}$ for each complainer. If formula ( 18) is not valid for all disputed shares, the $p_i$ is disqualified, and will be excluded from further computations. Let $Q_i$ be a set of all non-disqualified players.

• Key check: If party $p_j$ is found faulty, share $s_i$ is updated by removing it from $Q_i$ and recomputing the sum:$s_i=\sum_{j\in Q_i}{s_{ji}}$

• Key generation:

  • Compute public key: Each party can compute $A_{i0}$ and broadcast it. $A_{i0}=a_{i0}T$ Compute public key: $y_i=\sum_{j\in Q_i}^{ \, \bigoplus}{A_{j0}}$
  • Secret share: Each party their can compute their key share: $x_j=f_i(0)T$ And public key share: $s_j=\sum_{i\in Q_j}{s_{ij}}$
  • Recover: More than $t+1$ parties can recover the secret by using interpolation, as described in the following section.