Reputation system

The quality of services transacted on the Openfabric platform is subject to the quality of the ratings collected from endusers. The fundamental challenge is that a user can provide ratings that are not truthful to the actual experience that they had with the AI . When users provide ratings outside of the control of the relying party, it is difficult to know a priori when a user has submitted a dishonest evaluation. However, it is often the case that unfair evaluations diverge in their statistical patterns from those of the accurate and honest reviews [94]. Openfabric utilizes a Bayesian rating system [95] based on an analytical filtering technique, ensuring the exclusion of unfair ratings [96] [97]. The reputation score represents an indicator of how a particular AI, infrastructure, or dataset will behave in the future. Mathematically, the beta probability density function (PDF) can be defined using the gamma function Γ as:

$beta(p|\alpha, \beta)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}p^{\alpha-1}(1-p)^{\beta-1}$

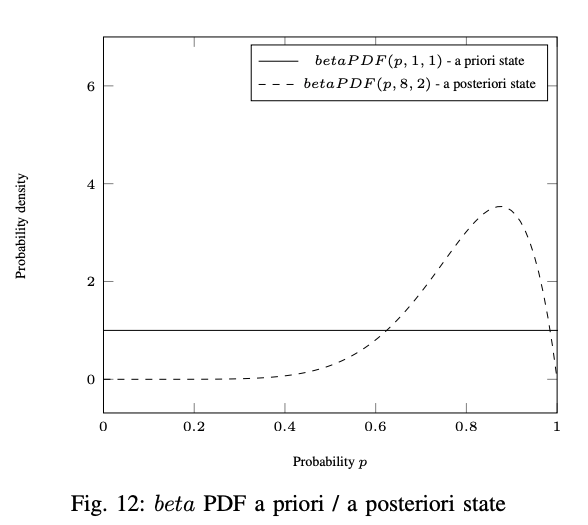
where $\alpha$ and $\beta$ represent the amount of positive and negative ratings. As depicted in Fig. 12, when nothing is known, the beta PDF has a uniform distribution where $\alpha=1$ and $\beta=1$.

The distribution readjusts after observing $r$ positive and $s$ negative evaluations. For example, the beta PDF after observing 7 positive and 1 negative ($\alpha=r+1$ and $\beta=s+1$) outcomes is illustrated in Fig. 12. $E(p)$ represents the probability expectation of the $beta$ function defined as:

$E(p)=\dfrac{\alpha}{(\alpha+\beta)}$

The rating system is composed of vectors $\rho=[r,s]$ where $r\geq0$ and $s\geq0$. The aggregated rating of service $Z$ at time $t_R$ performed by reviewers $X$ from the community $C$ is defined as:

$\rho^t(Z)=\sum_{X\in C}\rho^{X}_{Z,t_R}$

Taking into account that users may change their behavior over time, it might be advisable to favor more recent ratings over the ones that were cast further in the past. This can be achieved by including a survival factor $\lambda$ controlling the speed at which old ratings are "forgotten". The definition updates to:

$\rho^t(Z)=\sum_{X\in C}\lambda^{t-t_R}\rho^{X}_{Z,t_R}$

where $0\leq\lambda\leq1$ and $t$ is the current time. The reputation score of the agent $Z$ at time $t$ is defined as follows:

$R^t(Z)=E[ beta(\rho^t(Z)) ] = \dfrac{(r+1)}{(r+s+2)}$

Fig.12 - beta PDF a priori / a posteriori state

The pseudocode of the rating function is presented below:

$C$ is the set of all evaluators
$F$ is the set of all assumed fair raters
$Z$ is the evaluated agent
$F = C$
WHILE F changes do
    $\rho^t(Z)=\sum_{X\in F}\rho^{t}(X)$
    $R^t(Z)= E(\rho^t(Z))$
    FOR  rate R in F do
        $f=$ beta$(\rho^t(R,Z))$
        $l=$ q quantile of f
        $u=$ 1-q  quantile of f
        IF  $l<$ $R^t(Z)$ or  $u<R^t(Z)$  then
            F $= \setminus {R} $
        ENDIF
    ENDFOR
ENDWHILE
return $R^t(Z)$

The flexibility and robustness of this algorithm is ensured by variable distributions, rather than by a fixed threshold. If the spread of ratings from all reviewers is wide, then it will tend not to reject individual evaluators. If a rating vector $\rho=[r,s]$ is frequent among reviewers (e.g. 85% positive, 15% negative ratings) except for one reviewer ( e.g. 50% positive, 50% negative ratings), then the exceptional rating will be rejected. The algorithm’s sensitivity can be increased or decreased by modifying the $q$ parameter.